Plücker Coordinates and Geometric Algebra
Plücker coordinates are a way to represent lines in 3-D space. Like quaternions, they are traditionally treated as a somewhat mysterious but very useful way to augment standard linear algebra methods. In the context of geometric algebra Plücker coordinates become much more intuitive to understand. Also, the geometric algebra framework extends the concept of Plücker coordinates considerably, just as it does for quaternions. Here are some insights gleaned from our book.
This representation of lines is useful because it allows for compact formulation of solutions to various geometric problems such as:
- line-line intersection (meet).
- line-plane intersection (meet).
- point-line union (join).
However, Plücker coordinates are just one special case of representing k-dimensional linear subspaces. Using geometric algebra, any k-dimensional linear subspace can be represented as a computational element called a blade, and you won't need the lookup tables anymore because equations will become intuitive, simple and generic.
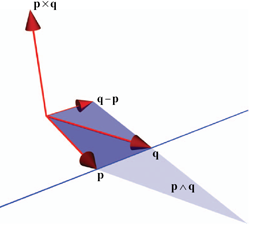
In geometric algebra, blades are constructed using the outer product (denoted ∧). For example, the subspace containing two vectors p and q is represented by the blade L = p ∧ q. The outer product is linear and anti-symmetric (so that p∧q = - q∧p, and p∧p = 0).
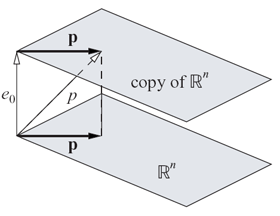
p = e0 + p
q = e0 + q
(e0 is a vector representing the point at the origin, so p and q are in fact 4-D homogeneous vectors whose w coordinate is 1).
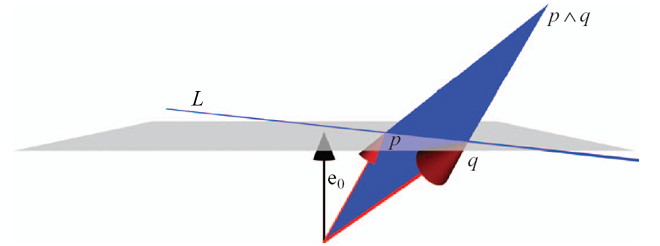
Now the outer product L = p ∧ q represents the line through p and q, as illustrated in Figure 11-2a below.
Because L is a 2-blade (a 2 dimensional blade) in 4-D space, it turns out to have six (Plücker) coordinates (but in general you don't much care about such implementation details because the formulation of geometric algebra is coordinate free).
If we write out L = p ∧ q , we obtain the Plücker coordinates formulation:
L = p∧q
= (e0+p)∧(e0+q)
= p∧q + p∧e0 + e0∧q
= p∧q + e0∧(q-p).
We recognize q-p as the direction of the line while p∧q is effectively the moment
of the line (p∧q is the 'dual' of p�q).
Note that nothing restricts us to 3-D Euclidean space (4-D homogeneous coordinates). If you need to do Euclidean geometry in, say, 7-D, geometric algebra lets you do so straightforwardly, without ever having to consider what the Plücker coordinates of a 7-D line look like in detail (and effortlessly computing the moment, even though there is no cross product in 7-D).
But this method to represent subspaces doesn't stop at lines. The outer product of three homogeneous points is a 3-blade which represents a plane: P = p ∧ q ∧ r. And of course, you can also construct a plane from a line and a point using P = L ∧ r. Such a plane has four homogeneous coordinates, which are classically thought of as 3 coordinates for the normal vector of the plane and one for its distance to the origin.
Even better, in the conformal model, points are defined such that the outer product of three collinear points represents a line through these points, and the outer product of three non-collinear points represents a circle through these three points! Hence circles and spheres have 'Plücker coordinates' too, and we can apply all the geometric computations in the list below to them.
Another great thing about the way geometric algebra handles subspaces is that you won't need to look up the elementary operations such as intersection anymore. These equations become simple and intuitive in geometric algebra, and they work for all combinations of arguments (in their own space). For example:
- Join (linearized union): J = A ∧ B.
- Meet (linearized intersection): M = A* ⋅ B.
- There are efficient general algorithms for true union (join) and intersection (meet) of any combination argument blades.
- Projection: P = (A . B-1) ⋅ B.
- Conformal rotor (this includes rotation, translation and scaling) which transforms primitive A into primitive B: √(B/A).
Note that computing this square root is straightforward and efficient ). - Applying a conformal rotor R to any primitive A: R A R-1.
As we saw in the last two list items, rotors (generalized quaternions in geometric algebra) and blades interoperate seamlessly because they are part of the same algebra. This means that you can easily rotate or translate lines, planes, circles and so on, always using the same rotor on each.
Bottom Line
When embedded and understood from a geometric algebra context, Plücker coordinates become a part of a framework which is both more intuitive to understand and much more powerful:- Usable for any affine subspace in n-D space, instead of being restricted to lines 3-D.
- Equations for construction, intersection, et cetera are simple and generic. This makes them easy to memorize, apply and use in further computations.
- Quaternions (rotors) can be straightforwardly applied to geometric primitives, since they are a part of the same geometric algebra.
- In the conformal model, circles and spheres have 'Plücker coordinates' too, and they work in the same way as lines and planes do.


